Нерівність трикутника один із найважливіших геометричних фактів – документ
Геометричні нерівності.
Під час вивчення математики учням часто доводиться стикатися з розв'язанням нерівностей. Одними з найскладніших видів нерівностей єгеометричні. У школі з їхньої вирішення приділяється мало часу, тому під час роботи з подібними нерівностями в учнів виникають труднощі. Однак на вступних іспитах до ВНЗ та на математичних олімпіадах такого роду завдання можна зустріти досить часто. Розглянемо деякі з них.
Нерівність трикутника
Теорема (нерівність трикутника):
Кожна сторона трикутника менша за суму двох інших його сторін.
Зауваження. Іноді використовують також і дещо інше формулювання цієї теореми, включаючи принагідно і випадок виродженого трикутника:
Довжинабудь-який Сторони трикутника завжди не перевищує суму довжин двох його інших сторін.
Зауважимо, що різниця між двома наведеними формулюваннями настільки незначна, що немає сенсу розглядати їх окремо. Надалі під час вирішення завдань ми використовуватимемо як перше формулювання теореми, і друге, не обумовлюючи це окремо.
Нерівність трикутника виникла, зважаючи на все, тоді ж, коли людина навчилася ходити і хоч якось мислити. Відомо, що з перших його формалізацій наводить Евклід у знаменитих «Початках». Там він доводить нерівність трикутника в такий спосіб. Спочатку доводиться теорема у тому, що зовнішній кут трикутника більше внутрішнього кута, із нею суміжного. З неї виводиться теорема у тому, проти більшої боку трикутника лежить більший внутрішній кут. Далі, шляхом протилежного доводиться теорема у тому, що проти більшого внутрішнього кута трикутника лежить велика сторона. А з цієї теореми виводиться нерівність трикутника. Ось такий непростий логічний ланцюжок для доказу цілком очевидної, здавалося б, нерівності!
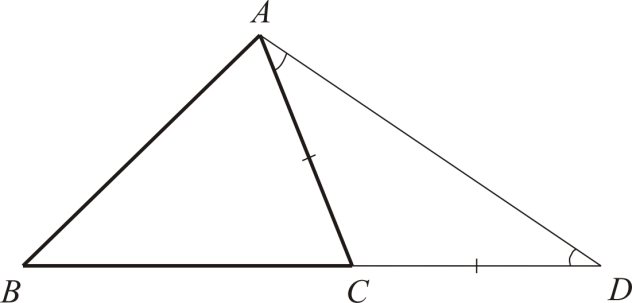
Доказ теореми . Розглянемо трикутник ABCі покажемо, що AB AC + BC. За доказом скористаємося одним із видів додаткових побудов – відкладанням рівних відрізків ( метод спрямування).
У трикутнику ABC(рис. 1) на продовженні сторони BCвідкладемо відрізок CD, рівний AC. В рівнобедреному трикутнику ACD  . У трикутнику ABDкут ADBменше кута BADзначить, BD AB, або BC + CD AB. Але CD = ACзначить, AC + BC AB.
. У трикутнику ABDкут ADBменше кута BADзначить, BD AB, або BC + CD AB. Але CD = ACзначить, AC + BC AB.
Зауваження. Зверніть увагу, що, виходячи з формулювання теореми, слід записати відразу три нерівності:
AB AC + BC ;
AC AB + BC ;
BC AB + AC .
Нерідко, записавши одну нерівність, про двох інших чомусь забувають. Пам'ятайте, що це може призвести до неприємних помилок.
Нерівність трикутника може бути одним із простих критеріїв приналежності трьох точок однієї прямої. Три точки будуть належати одній прямій тоді й лише тоді, як у нерівності трикутника досягається рівність. Звичайно, рівність може досягатися лише в одному з трьох нерівностей (див. зауваження), оскільки одна з точок лежатиме чітко між двома іншими.
Доведіть, що у трикутнику кожна сторона більша за різницю двох інших сторін.
Наведемо як приклад використання нерівності трикутника кілька порівняно нескладних геометричних завдань.
(a , b , c - Сторони трикутникаABC ).
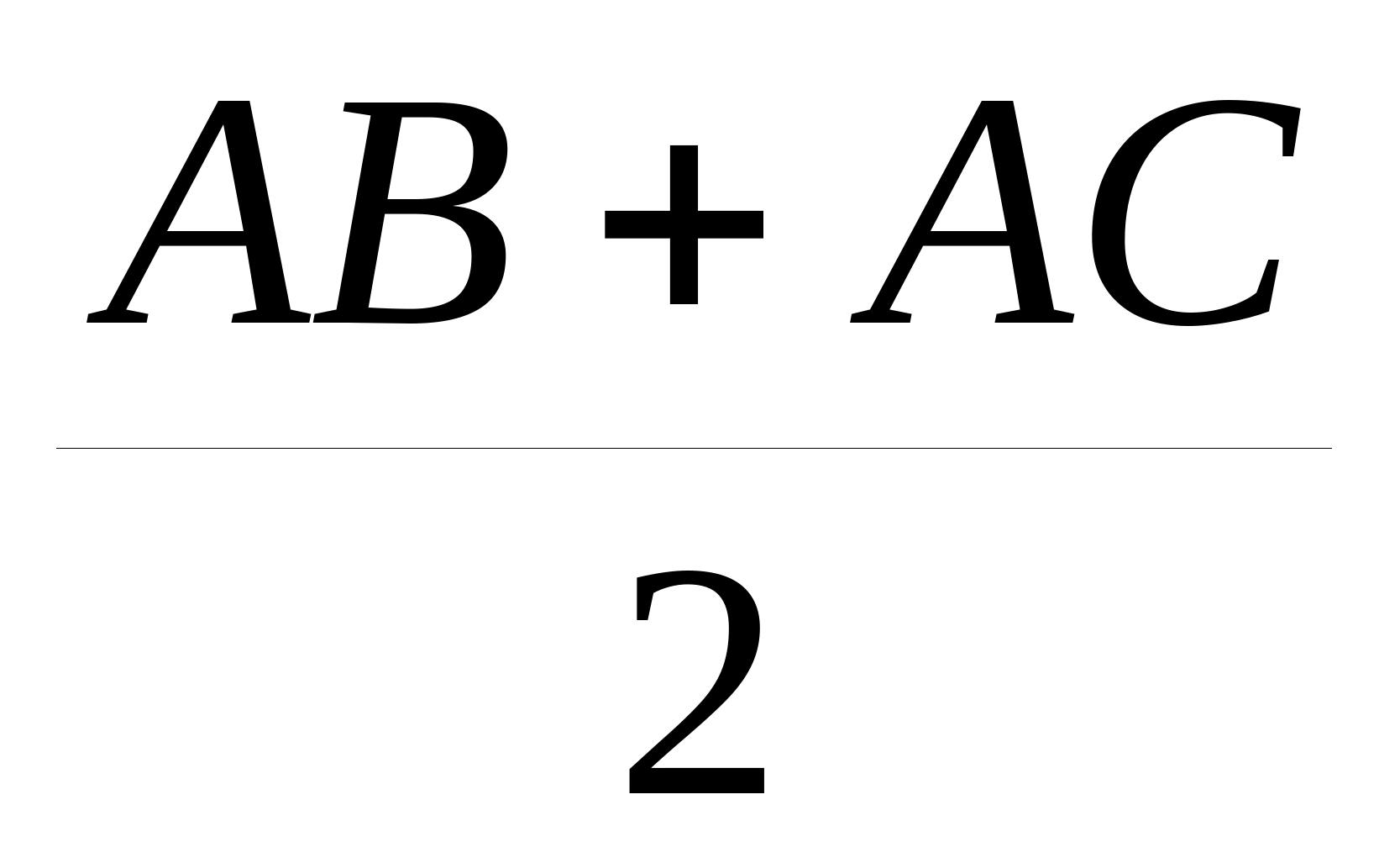
a ( b - c ) 2 + b ( c - a ) 2 + c ( a - b ) 2 + 4 abc a 3 + b 3 + c 3 .
a , b іc
a , b іc - Довжини сторін довільного трикутника. Доведіть, що
( a + b - c )( a - b + c )(- a + b + c ) abc .
a, bі c- Довжини сторін довільного трикутника. Доведіть, що
a 2 b (a - b ) + b 2 c (b - c ) + c 2 a (c - a ) 0.
Довжини двох сторін трикутника a та b задовольняють умові a b, а довжини відповідних їм висот дорівнюють haі hb.
Довести нерівність a + ha≥ b + hbі визначити, коли досягається рівність.
Доведіть, що сума довжин будь-яких двох медіан довільного трикутника
а) не більше ¾P
, деP
– периметр цього трикутника;
б) не менше ніж ¾p
, деp
- Напівпериметр цього трикутника.
Рішення
Побудуємо відрізок CB 1 так, що чотирикутник ABB 1 C– паралелограм, тоді AC=BB 1 . З трикутника BB 1 Dотримуємо, що BB 1 +BD B 1 Dі, отже, AC+BD B 1 D. Залишається помітити, що трикутник CB 1 Dрівносторонній ( CD=CB 1 = 1 , а B 1 CD= AOC= 60 o ), і, отже, B 1 D= 1 . Таким чином, отримуємо AC+BD 1 .
Рішення
Візьмемо на сторони AB, BC, CAточки C 2 , A 2 , B 2 так, що A 1 B 2 | AB, B 1 C 2 | BC, C 1 A 2 | CA(Рис.). Тоді A
1
B
1
A
1
B
2
+
B
2
B
1
= (1 - )
AB
+ (2 - 1)
CA. Аналогічно B
1
C
1
)
BC
+ (2 - 1)
ABі C
1
A
1
)
CA
+ (2 - 1)
BC. Складаючи ці нерівності, отримуємо P 1 P.
Ясно що A 1 B 1 + A 1 C B 1 C, тобто. A
1
B
1
+ (1 - )
BC
.
CA. Аналогічно B
1
C
1
+ (1 - )
CA
.
ABі C
1
A
1
+ (1 - )
AB
.
BC. Складаючи ці нерівності, отримуємо P 1 (2 - 1)P.
Математичний гурток Русанівського ліцею
Нерівність трикутника
Нерівність трикутника – один із найважливіших геометричних фактів. Є однією з інтуїтивних властивостей відстані, вона нерідко допомагає у вирішенні непростих геометричних і текстових завдань. За допомогою нерівності трикутника можна відсіяти частину з можливих варіантів розташування будь-яких елементів у громіздких геометричних задачах. Часто саме невиконання суворої нерівності трикутника (а саме – досягнення в ньому рівності) дає підстави стверджувати про належність трьох точок однієї прямої. Таким чином, нерівність трикутника є одночасно інтуїтивно зрозумілою, навіть очевидною, але часто стає потужним інструментом при вирішенні серйозних математичних завдань.
Декілька слів про нерівності
В математиці нерівністьє твердження про відносну величину або порядок двох об'єктів, що розглядаються, або про те, що вони просто не однакові. Класична нерівність як об'єкт дослідження можна також розглядати як окремий випадок відношення порядку. Розрізняють строгіі несуворінерівності. Або ж, переходячи на мову відносин, суворе нерівність можна вважати ставленням строгого порядку на безлічі дійсних чисел (тобто ставленням, яке має властивості антирефлексивності, антисиметричності та транзитивності). Якщо ж йдеться про несувору нерівність, то можна говорити про неї як про відношення нестрогого порядку на тій самій множині (тобто розглядати замість антирефлексивності рефлексивність). Нагадаємо, що про відносини як математичний об'єкт та їх властивості ми вже згадували в Лекції 7 (були розглянуті властивості відношення ділимості). Докладніше їх вивчення ми маємо в майбутньому, оскільки вони досить успішно систематизують і узагальнюють ряд елементарних математичних понять. Тепер ми наведемо кілька прикладів нерівностей кожного з названих типів. Сувориминерівностями називають такі нерівності:
- a < b- означає, що aменшеb; a
> b
- означає, що aбільшеb; a
≠ b- означає, що aне дорівнюєbабо ж що aі b різні.
- a ≤ b- означає, що aменше чи одноbабо, що те саме, aне більше (не перевищує, не перевищує)b; a ≥
b- означає, що aбільше чи одноbабо, що те саме, aне меншеb.
Нерівність трикутника
Теорема (нерівність трикутника): Кожнасторона трикутника менша за суму двох інших його сторін. Зауваження. Іноді використовують також і дещо інше формулювання цієї теореми, включаючи принагідно і випадок виродженого трикутника: Довжина будь-якийСторони трикутника завжди не перевищує суму довжин двох його інших сторін. Зауважимо, що різниця між двома наведеними формулюваннями настільки незначна, що немає сенсу розглядати їх окремо. Надалі під час вирішення завдань ми використовуватимемо як перше формулювання теореми, і друге, не обумовлюючи це окремо. Нерівність трикутника виникла, зважаючи на все, тоді ж, коли людина навчилася ходити і хоч якось мислити. Відомо, що з перших його формалізацій наводить Евклід у знаменитих «Початках». Там він доводить нерівність трикутника в такий спосіб. Спочатку доводиться теорема у тому, що зовнішній кут трикутника більше внутрішнього кута, із нею суміжного. З неї виводиться теорема у тому, проти більшої боку трикутника лежить більший внутрішній кут. Далі, шляхом протилежного доводиться теорема у тому, що проти більшого внутрішнього кута трикутника лежить велика сторона. А з цієї теореми виводиться нерівність трикутника. Ось такий непростий логічний ланцюжок для доказу цілком очевидної, здавалося б, нерівності!|
|
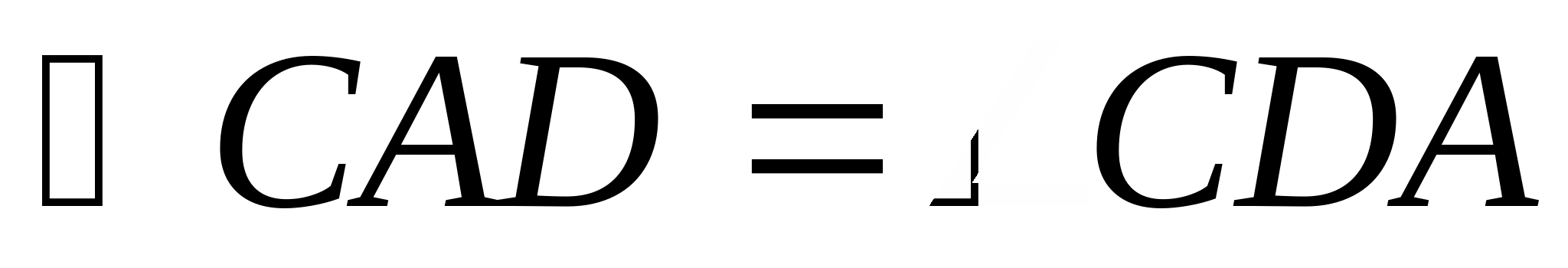 . У трикутнику ABDкут ADBменше кута BADзначить, BD > AB, або BC + CD
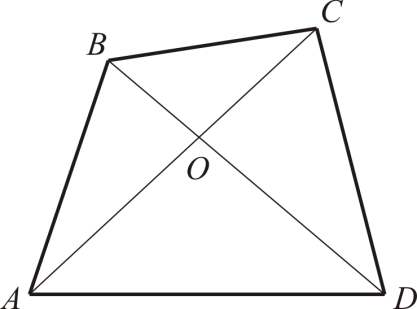
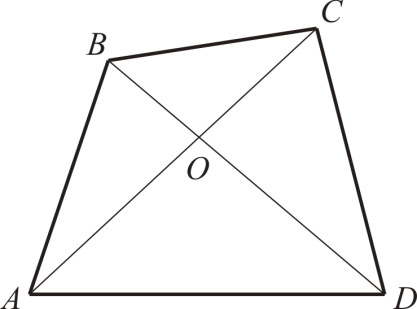
> AB. Але CD = ACзначить, AC + BC > AB. Зауваження. Зверніть увагу, що, виходячи з формулювання теореми, слід записати відразу три нерівності: AB < AC + BC; AC< AB + BC; BC < AB + AC. Нерідко, записавши одну нерівність, про двох інших чомусь забувають. Пам'ятайте, що це може призвести до неприємних помилок. Нерівність трикутника може бути одним із простих критеріїв приналежності трьох точок однієї прямої. Три точки будуть належати одній прямій тоді й лише тоді, як у нерівності трикутника досягається рівність. Звичайно, рівність може досягатися лише в одному з трьох нерівностей (див. зауваження), оскільки одна з точок лежатиме чітко між двома іншими. Вправа. Доведіть, що у трикутнику кожна сторона більша за різницю двох інших сторін. Наведемо як приклад використання нерівності трикутника кілька порівняно нескладних геометричних завдань. Завдання 1. Доведіть, що у довільному чотирикутнику ABCD AB + CD < AC + BD.
. У трикутнику ABDкут ADBменше кута BADзначить, BD > AB, або BC + CD
> AB. Але CD = ACзначить, AC + BC > AB. Зауваження. Зверніть увагу, що, виходячи з формулювання теореми, слід записати відразу три нерівності: AB < AC + BC; AC< AB + BC; BC < AB + AC. Нерідко, записавши одну нерівність, про двох інших чомусь забувають. Пам'ятайте, що це може призвести до неприємних помилок. Нерівність трикутника може бути одним із простих критеріїв приналежності трьох точок однієї прямої. Три точки будуть належати одній прямій тоді й лише тоді, як у нерівності трикутника досягається рівність. Звичайно, рівність може досягатися лише в одному з трьох нерівностей (див. зауваження), оскільки одна з точок лежатиме чітко між двома іншими. Вправа. Доведіть, що у трикутнику кожна сторона більша за різницю двох інших сторін. Наведемо як приклад використання нерівності трикутника кілька порівняно нескладних геометричних завдань. Завдання 1. Доведіть, що у довільному чотирикутнику ABCD AB + CD < AC + BD. |
|
AO + OB > AB;
CO + OD > CD.
Розглянемо суму AC + BD:
AC + BD = (AO + OC) + (BO + OD) =
= (AO + BO) + (OC + OD) > AB + CD.
Завдання 2. Доведіть, що у трикутнику ABCвиконано нерівність ( a, b, c- Сторони трикутника ABC). Рішення . Скористаємося наслідком із нерівності трикутника (див. вправу):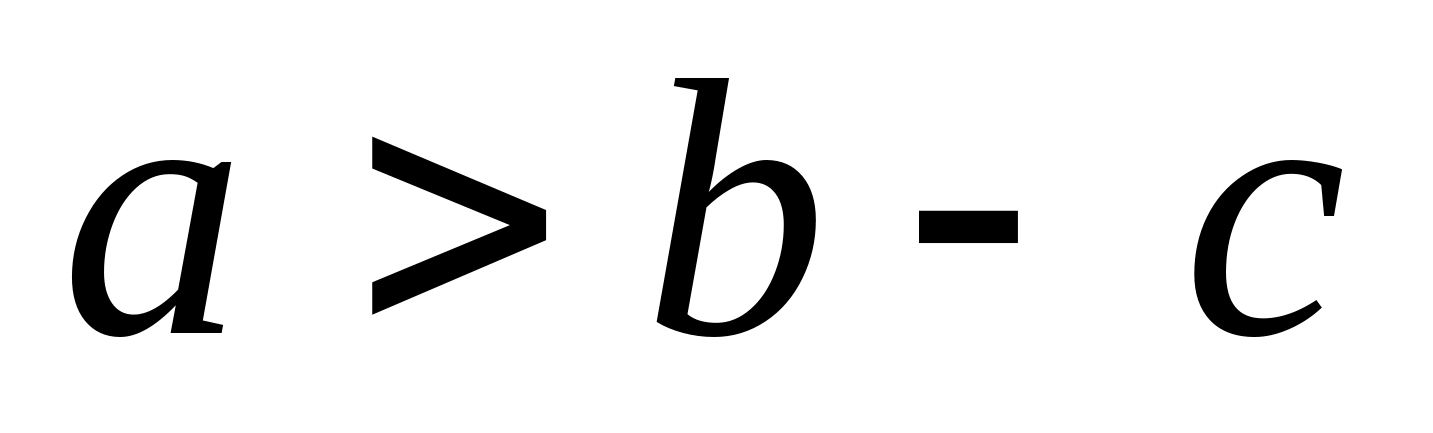 (Припускаємо, що
(Припускаємо, що 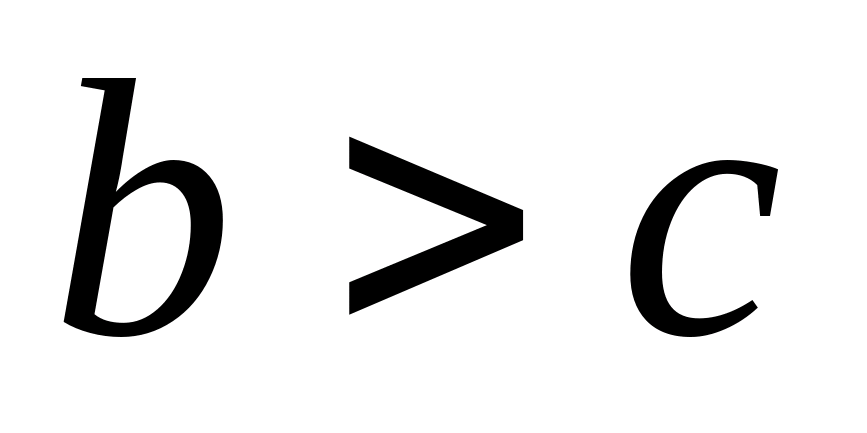 ). Тоді, звівши в квадрат обидві частини нерівності, отримаємо:
). Тоді, звівши в квадрат обидві частини нерівності, отримаємо: Аналогічно:
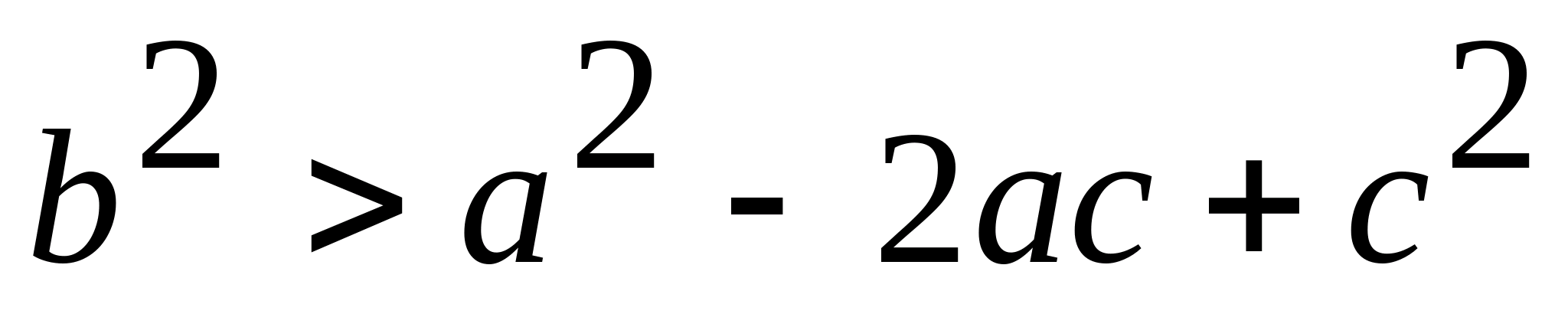 ;
;
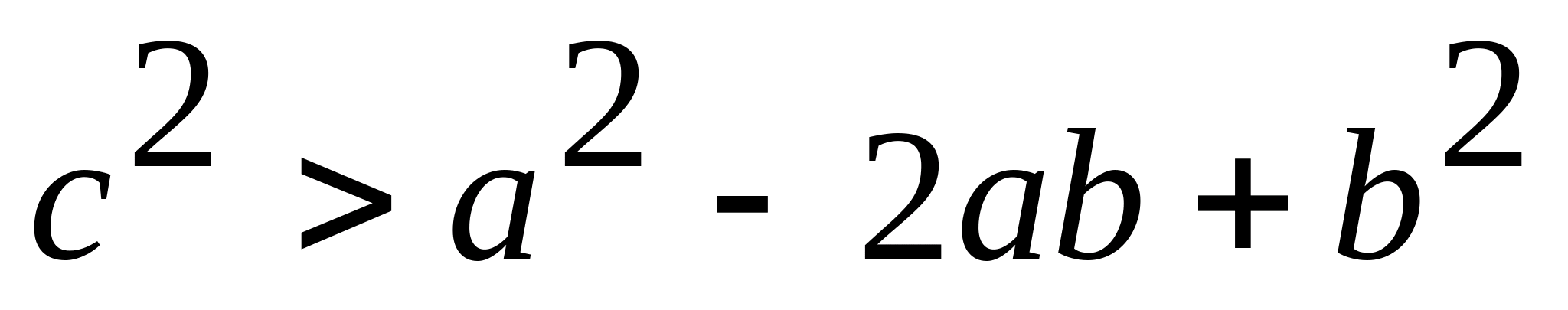 .
.
Складаючи всі три нерівності, отримаємо потрібне. Вправа. Доведіть, що медіана AMу довільному трикутнику ABCза довжиною менше, ніж 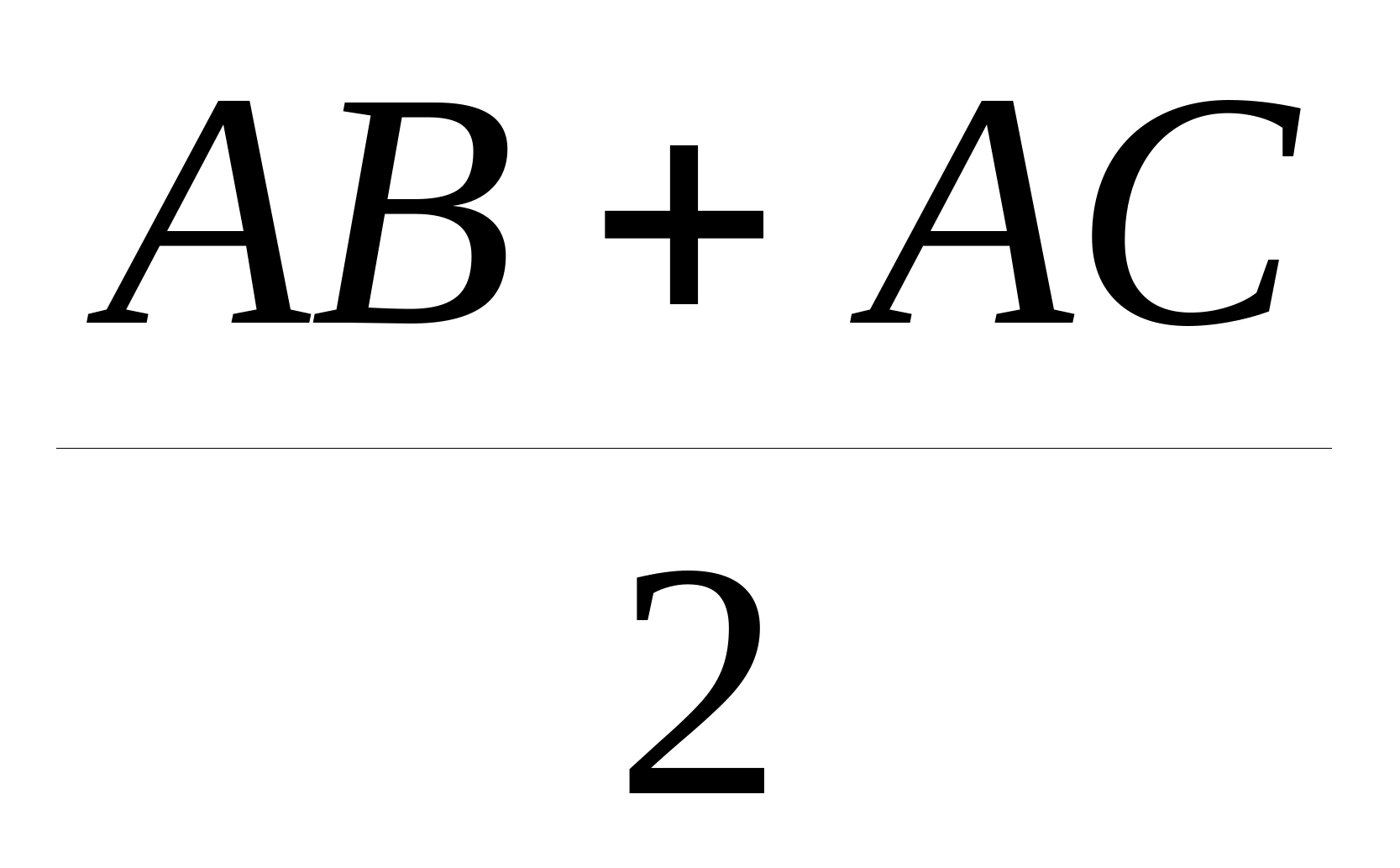 . Завдання 3. На площині дано квадрат ABCDі крапка O. Доведіть, що відстань від точки Oдо однієї з вершин квадрата не перевищує суми відстаней від Oдо трьох інших вершин квадрата. Рішення
. Складіть нерівності трикутника AC + OC > OAі OB + OD > BD. Так як AC = BD, то, скорочуючи, отримуємо потрібне. Завдання 4. Знайдіть усередині опуклого чотирикутника точку, таку, що сума відстаней від неї до вершин мінімальна. Рішення
. Так як чотирикутник опуклий, його діагоналі перетинаються в точці Oусередині нього. Позначимо вершини чотирикутника через A, B, Cі D(за годинниковою стрілкою). Тоді сума відстаней від Oдо вершин дорівнює сумі довжин діагоналей ACі BD. Але для будь-якої іншої точки Pмаємо, по-перше, що сума відстаней від Pдо вершин не менше AC + BD, а по-друге, або PA + PC > AC, або PB + PD > BD. Отже, ця сума дорівнює AC + BDтільки якщо Pзбігається з точкою O. Значить, точка O- Шукана. Нерівність трикутника успішно застосовується й у досить заплутаних текстових задачах. Що цікаво, у таких завданнях багато може залежати від того, наскільки вдало Ви побудуєте геометричну інтерпретацію. Завдання 5. У деякій країні розташовані 4 міста: A, B, Cі D. Два літаки одночасно вилетіли із міста A. Маршрут першого літака: A-B-D-C-A-D-B-C-A, А маршрут другого: A-B-C-D-A-B-C-D-A-B-C-D-A. Який із літаків раніше закінчить свій маршрут, якщо їхні швидкості однакові? Не бійтеся експериментувати! Якщо в задачі не задано конкретне розташування об'єктів, Ви маєте право малювати у своєму рішенні все, що не суперечить умові - адже воно Ваше. В тому числі міста в Задачі 5 Ви можете розставити як завгодно. Слід пам'ятати, що у деяких завданнях після розбору «нормального», загального випадку, необхідно розібрати і деякі «патологічні», окремі випадки. Наприклад, у Завданні 5 може знадобитися розгляд випадку, коли деякі три міста лежать на одній прямій – все залежить від того, яке рішення для загального випадку. Розв'язання задачі 5
. Запишемо довжини маршрутів кожного з літаків як сум відстаней між містами. Довжина маршруту першого літака дорівнюватиме
. Завдання 3. На площині дано квадрат ABCDі крапка O. Доведіть, що відстань від точки Oдо однієї з вершин квадрата не перевищує суми відстаней від Oдо трьох інших вершин квадрата. Рішення
. Складіть нерівності трикутника AC + OC > OAі OB + OD > BD. Так як AC = BD, то, скорочуючи, отримуємо потрібне. Завдання 4. Знайдіть усередині опуклого чотирикутника точку, таку, що сума відстаней від неї до вершин мінімальна. Рішення
. Так як чотирикутник опуклий, його діагоналі перетинаються в точці Oусередині нього. Позначимо вершини чотирикутника через A, B, Cі D(за годинниковою стрілкою). Тоді сума відстаней від Oдо вершин дорівнює сумі довжин діагоналей ACі BD. Але для будь-якої іншої точки Pмаємо, по-перше, що сума відстаней від Pдо вершин не менше AC + BD, а по-друге, або PA + PC > AC, або PB + PD > BD. Отже, ця сума дорівнює AC + BDтільки якщо Pзбігається з точкою O. Значить, точка O- Шукана. Нерівність трикутника успішно застосовується й у досить заплутаних текстових задачах. Що цікаво, у таких завданнях багато може залежати від того, наскільки вдало Ви побудуєте геометричну інтерпретацію. Завдання 5. У деякій країні розташовані 4 міста: A, B, Cі D. Два літаки одночасно вилетіли із міста A. Маршрут першого літака: A-B-D-C-A-D-B-C-A, А маршрут другого: A-B-C-D-A-B-C-D-A-B-C-D-A. Який із літаків раніше закінчить свій маршрут, якщо їхні швидкості однакові? Не бійтеся експериментувати! Якщо в задачі не задано конкретне розташування об'єктів, Ви маєте право малювати у своєму рішенні все, що не суперечить умові - адже воно Ваше. В тому числі міста в Задачі 5 Ви можете розставити як завгодно. Слід пам'ятати, що у деяких завданнях після розбору «нормального», загального випадку, необхідно розібрати і деякі «патологічні», окремі випадки. Наприклад, у Завданні 5 може знадобитися розгляд випадку, коли деякі три міста лежать на одній прямій – все залежить від того, яке рішення для загального випадку. Розв'язання задачі 5
. Запишемо довжини маршрутів кожного з літаків як сум відстаней між містами. Довжина маршруту першого літака дорівнюватиме
Другий літак пролетить відстань
Розглянемо різницю між відстанню, що пролетів перший літак, та відстанню, яку подолав другий.
Доведемо, що незалежно від розташування точок A, B, C, Dна площині (міст A, B, C, Dкраїни) вираз буде позитивним. Для цього слід розглянути два випадки. 1. Припустимо, що точки A, B, C, D ABCDз діагоналями ACі BD. Тоді запишемо послідовно нерівності трикутника для трикутників ABC, BCD, CDAі DAB(див. рис. 2):
AB + BC > AC;
BC + CD > BD;
CD + DA > CA;
DA + AB > DB.
Склавши всі чотири нерівності, отримаємо
2. Розглянемо випадок, коли точки A, B, C, D створюють на площині чотирикутник ACBDз діагоналями ABі CD (Намалюйте собі відповідний малюнок). Зауважимо, що нерівності трикутника виконуються тих самих трикутників, що у першому випадку. Виявляється, що розв'язання задачі залишиться тим самим, незважаючи на те, що розташування точок на площині суттєво змінилося. Це можна вважати ще однією характерною рисоюбагатьох розв'язків задач, що використовують нерівність трикутника. Отже, перший літак прилетить раніше, оскільки його маршрут коротший за маршрут другого. Зауважте, що розв'язання Завдання 5 потребує невеликого аналізу, що є неодмінною якістю всіх олімпіадних завдань. Будьте уважні – Ваше вирішення завдання буде правильним лише тоді, коли Ви розглянете усі можливі випадки, які підходять під умову. Слід також відзначити, що часто на малюнку, що зображує умову задачі, не видно трикутника, застосування нерівності трикутника якого дало б моментальне рішення. У такому разі може допомогти успішно підібране геометричне перетворення. Про це ми поговоримо трохи згодом. Знайомство з нерівністю трикутника у цьому слід оголосити закінченим. Але нова зустріч із ним уже не за горами. 7 клас Лекція 13. Нерівність трикутника
Фіхте Йоганн Готліб (1762-1814) - один з найвизначніших представників класичної німецької філософії. До книги увійшли відомі роботи: «Факти свідомості», «Призначення людини», «Науковчення» та інші книги
КнигаФіхте Йоганн Готліб (1762-1814) - один із найвизначніших представників класичної німецької філософії. До книги увійшли відомі роботи: "Факти свідомості", "Призначення людини", "Наукоучення" та інші.
Жозеф Артур Гобіне. Досвід про нерівність людських рас
КнигаЯким би зловісним не представлявся у ЗМІ та літературі нинішньому та минулому поколінням націонал-соціалізм, він не перестає привертати до себе уваги мільйонів людей.
Пентаграма одна із найважливіших магічних символів. Саме це слово походить від грецьких слів "pente", що означає п'ять, і "gramma" літера
ДокументСимвол захисту і влади - ПентаграмаМарсія Пентаграма є одним з найважливіших магічних символів. Саме це слово походить від грецьких слів "pente", що означає п'ять, і "gramma" - літера; пентаграма -
Відеоурок «Нерівність трикутника» розкриває зміст та доказ теореми про нерівність трикутника. Завдання даного відеоуроку - полегшити запам'ятовування теореми та наслідки з неї, розуміння та запам'ятовування перебігу міркувань за її доказом.
Високий рівень наочності матеріалу, голосовий супровід дає можливість використовувати цей посібник як самостійну частину уроку, звільняючи час вчителя для поліпшення якості навчання, посилення індивідуальної роботи з учнями.
Відеоурок починається з представлення теми та формулювання теореми про нерівність трикутника. Для запам'ятовування затвердження теореми вона виведена на екран та виділена кольором. Ця теорема стверджує, що будь-яка сторона трикутника є меншою від суми двох інших його сторін. Доказ затвердження пропонується розглянути на прикладі трикутника Δ, який демонструється під текстом теореми на екрані.
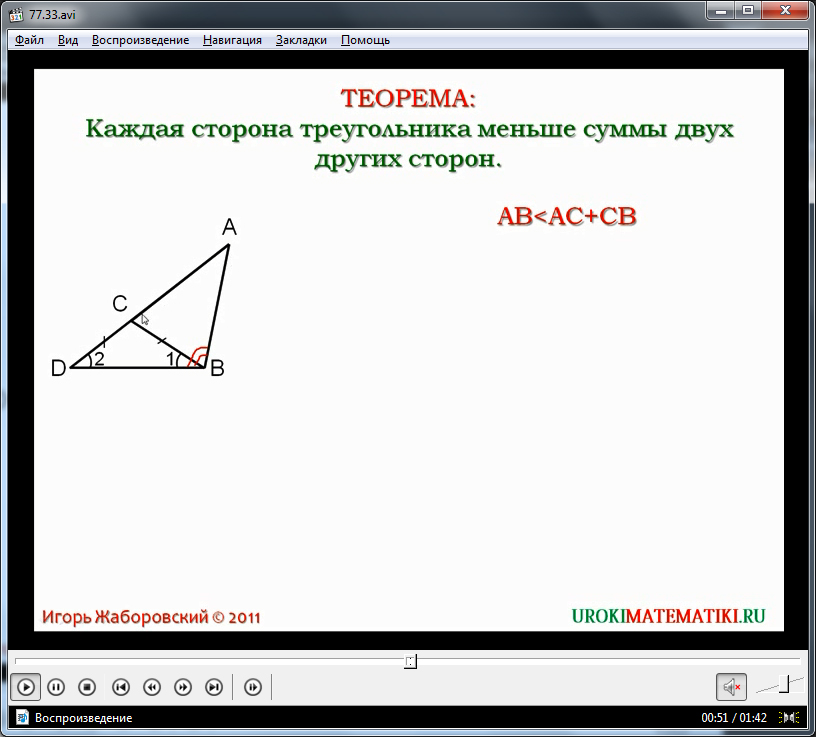
Уточнюється, що для доказу теореми необхідно підтвердити, що сторона AB є меншою за величину суми сторін AC і CB. Дане твердження позначено на екрані виразом AB Освоївши цю теорему, можна розглядати її слідство, яке стверджує, що для будь-яких трьох точок A, B, C, які не належать до однієї прямої, справедливі нерівності: AB Відеоурок «Нерівність трикутника» може бути використаний вчителем на уроці геометрії як наочний посібник або як частина уроку замість пояснення вчителем нової теми. Детальне зрозуміле пояснення замінить вчителя при самостійному вивченні предмета учнем, і навіть допоможе пояснити предмет під час дистанційного навчання. Мета уроку:вивчити теорему про нерівність трикутника і показати її застосування під час вирішення завдань. Завдання: Тип уроку:урок вивчення та первинного закріплення нових знань. Обладнання:дошка, комп'ютер, інтерактивна дошка або мультимедійний проектор, презентація, підручники, робочі зошити ( Додаток 1
), 14 наборів смужок з картону по 5 см, 7 см (2 шт.), 9 см, 12 см, 14 см, 16 см, таблички з трикутниками, смайли ( Додаток 2
). ХІД УРОКУ 1. Організаційний етап 2. Підготовка до основного етапу уроку(Забезпечення мотивації та прийняття учнями мети навчально-пізнавальної діяльності, актуалізація опорних знань) – Подивіться на малюнок, виконаний на дошці. Як називається ця постать? (Це трикутник.) 3.Засвоєння нових знань та способів дій 3.1. Постановка проблеми, висунення гіпотези Якби тільки мене спитали, Де вулкани дряпають небо – Ці чудові вірші Анатолія Старікана присвячені нашій малій батьківщині Камчатці. Камчатка має свої традиції і однією з них є щорічне проведення Берінгії. – Зазвичай Берінгія проводиться у березні і разом із початком весни приходить у населені пункти на своєму шляху, приносячи радість їхнім мешканцям. Варто зауважити, що гонка, крім змагальної складової, має ще й гуманітарне значення для жителів сіл та селищ Камчатського краю, де відпочивають учасники перегонів. Дітям та школам віддалених куточків Камчатки надають спонсорську допомогу. Проблемна ситуація. Яку фігуру потрібно побудувати, щоб вирішити цю проблему? (Потрібно побудувати трикутник.) Яка може бути довжина третьої сторони? Висловіть свої гіпотези, ми перевіримо їх наприкінці уроку. Дослідницька робота – Перед вами лежать макети сторін трикутників. а) 7, 12, 9; У першому завданні трикутник побудувати легко. У другій вийшов відрізок. Чому? (Т. К. Три вершини лежать на одній прямій, а трикутник - це фігура, складена з трьох точок, що не лежать на одній прямій, попарно з'єднаних відрізками. Довжина більшого відрізка дорівнює сумі довжин менших.) - Чи можна побудувати трикутник у третьому випадку? (У третьому випадку трикутник побудувати не можна, тому що довжина більшої сторони більша за суму довжин менших сторін.) Вчитель вислуховує версії учнів.У разі складнощів можна запропонувати дітям порівняти довжину сторони, побудованої першою та суму двох інших сторін трикутника. – Отже, трикутник, із якими сторонами ми змогли побудувати? (Трикутник зі сторонами 7, 12, 9) AB< BC + АС,
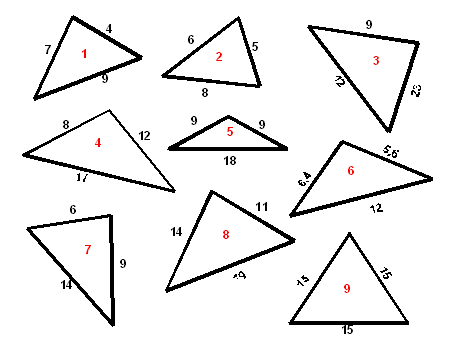
так як 9 см< 7 см + 12 см Учні позначають сторони трикутника, записують нерівності у зошиті. – Як називаються вирази, записані на дошці? (Нерівності.) Енергізатор Відкладіть ручки, поверніть пари обличчям один одному. На рахунок «один» підніміть праву руку з витягнутим вказівним пальцем. На рахунок «два» накрийте лівою долонею вказівний палець сусіда. На рахунок «три» встигніть прибрати свою руку і схопити палець сусіда. Почали! Хлопці із задоволенням виконують вправу, яка знімає напругу та створює доброзичливу атмосферу, підвищує енергетичний потенціал учнів. 3.3. Доказ теореми – Відкрийте підручник на стор. 74, прочитайте формулювання теореми про нерівність трикутника. Учні працюють над формулюванням теореми, з'ясовують, що дано і що потрібно довести, будують малюнок і доводять теорему разом з учителем у зошитах. Відповідають на запитання вчителя. Теорема.Кожна сторона трикутника менша за суму двох інших сторін. 4. Фізкультхвилина, повторення Переможцем Берінгії у 2011 році став каюр Карагінського району, і щоб дізнатися про ім'я переможця пограємо з вами в математичне поле чудес. Знаходьте відповіді на мої запитання на малюнках, розвішаних по периметру класу і називайте лише букву. (Хлопці грають стоячи.) – Цілком вірно, переможцем є Андрій Прітчин, який подолав увесь шлях за 90 годин. 5. Первинна перевірка розуміння та закріплення знань - Виберіть, які трикутники не існують? (Учні працюють самостійно, одна людина працює біля дошки, потім перевірка.) Відповідь: не існують трикутники з номерами 3, 5, 6 - Хлопці, що ви помітили? Як швидко застосувати теорему про нерівність трикутника? (Висловлюють свої версії.)– Сума двох сторін, має бути більшою за третю сторону. Наприклад, 10 + 3 > 5, але трикутник не можна побудувати, чому? (Оскільки 3 + 5< 10.) То есть, для того
чтобы быстро проверить существует ли
треугольник, надо сравнить большую сторону с
суммой двух меньших сторон. - Молодці, хлопці! Швидко впоралися із завданням! 6. Узагальнення та систематизація знань(вирішення проблеми, перевірка гіпотези) – Отже, яка умова має виконуватись, щоб можна було побудувати трикутник? (Велика сторона трикутника має бути меншою від суми двох менших сторін.) Додаткове завдання:із якою середньою швидкістю рухався переможець, якщо весь шлях він подолав за 90 годин? 7. Постановка домашнього завдання 8. Підсумки уроку, оцінка знань, рефлексія Фронтальним опитуванням вчитель разом із учнями підбиває підсумки уроку і активним хлопцям ставить оцінки. – Яку тему ми сьогодні вивчили? (Нерівність трикутника.) – Молодці! Андрій Прітчин є чотириразовим переможцем Берінгії, і я впевнена, що кожен з вас обов'язково стане переможцем у тій чи іншій галузі. Головне дуже захотіти і досягати поставленої мети. Література: Атанасян Л.С.та ін. Геометрія 7-9.: навч. для загальноосвіт.установ / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев та ін - М.: Просвітництво, 2006. Інтернет ресурси: З геометрії ми знаємо, що сума довжин двох сторін трикутника не менша за довжину його третьої сторони. Подивимося, як можна висловити цю теорему алгебраїчно. Розглянемо трикутник, розташований так, як показано на рис. 22. Геометрична нерівність рівносильно алгебраїчної нерівності трикутника Чи можна довести останню нерівність, не звертаючись до геометрії? У § 8 гол. III було наведено доказ для одновимірного випадку (див. теорему 2 гл. III). в якому нерівність набуває такого вигляду: у цьому записі воно зустрічається частіше, ніж рівносильна йому нерівність Найбільш простий спосіб доказу двовимірного варіанта нерівності трикутника (4.50) полягає в тому, щоб довести рівносильну йому нерівність. Рис. 22. Нерівність трикутника. Для цього зведемо обидві частини нерівності (4.50) у квадрат, при цьому ми прийдемо до нерівності рівносильному (4.50). Легко бачити, що остання нерівність у свою чергу рівносильна наступному: Але це нерівність є простим наслідком відомої нерівності Коші [двовимірний варіант, див. (4.38)] що й доводить нерівність трикутника. Як і в одномірному випадку, визначення умов, за яких нерівність трикутника (4.50) звертається в рівність, не становить особливих труднощів. Згадаймо, що у нерівності Коші (4.52) рівність досягається тоді й лише тоді, коли пропорційні, тобто коли Нерівність (4.51) може бути отримана шляхом вилучення квадратного кореня з обох частин нерівності (4.52). Ця операція законна, тому що мається на увазі невід'ємний квадратний корінь з виразу, що стоїть зліва. Нехай є негативний квадратний корінь з виразу, що стоїть у правій частині (4.52). І тут навіть тоді, коли пропорційні, в (4.51) матиме місце суворе нерівність. Таким чином, рівність (4.51), а отже, і в нерівності трикутника (4.50) досягається тоді і тільки тоді, коли де неотрицательный коефіцієнт пропорційності. Геометричний сенс цієї умови, необхідної і достатньої для того, щоб у формулі (4.50) мала місце рівність, полягає в наступному: точки (рис. 21) повинні належати одній прямій, причому точки розташовані по одну сторону від точки О. При трикутник перетворюється на відрізок прямий. Інакше висловлюючись, точки як лежать однією прямої з точкою Про, а й лежать одному промені з початком Про. Легко переконатися в тому, що отримані умови узгоджуються з відповідними умовами для одновимірного випадку (нерівності де рівність досягається тоді і тільки тоді, коли числа мають один знак. Доказ нерівності трикутника можна узагальнити, слідуючи тим самим шляхом, що і при виведенні нерівності Гельдера, а саме довести, що нерівність має місце для будь-яких дійсних значень причому, як і раніше, рівність досягається в тому і лише тому випадку, коли числа пропорційні і коефіцієнт пропорційності позитивний. Ми повернемося до цієї нерівності в гол. VI, де буде розглянуто його геометричне значення. Перейдемо до іншого доказу нерівності трикутника, яке можна використовувати також для отримання більш загальних результатів. Має місце тотожність Нерівність Коші у формі, що використовує квадратне коріння [див. (4.51)], застосуємо по черзі до двох виразів.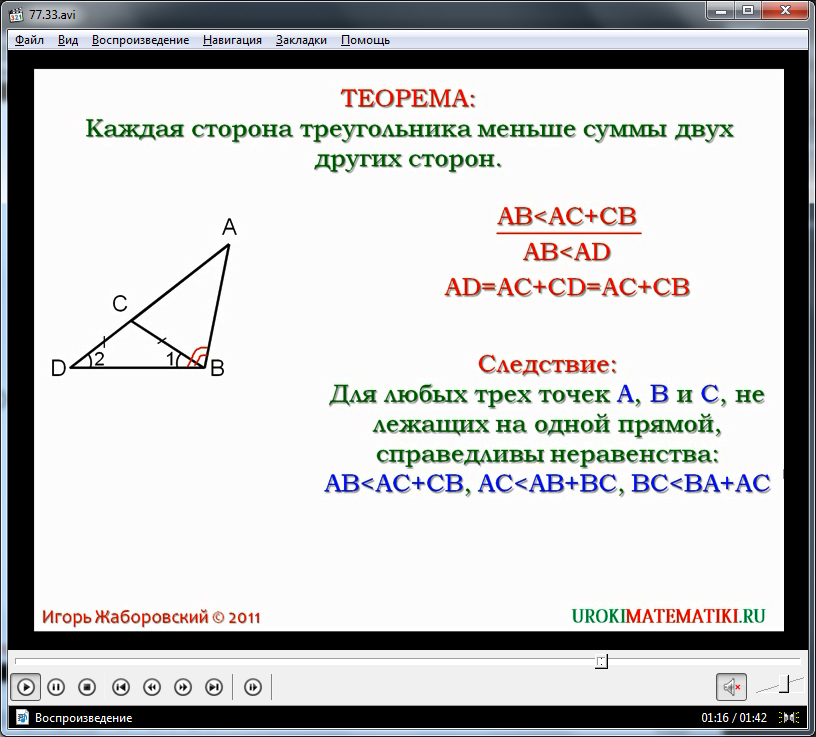
![]()
– Яка постать називається трикутником? (Трикутник – фігура, що складається з трьох точок, що не лежать на одній прямій та трьох відрізків, що попарно з'єднують ці точки.)
- Що виникає у вашій пам'яті? Що ви можете розповісти про цей трикутник? Якщо позначити трикутник АВС, назвіть велику сторону. (Хлопці відповідають питання вчителя.)
– А чому саме цю фігуру я запропонувала вам згадати? (Вивчатимемо якісь властивості трикутника.)
– Цілком вірно, сьогодні ми вивчатимемо властивість «нерівність трикутника».
Я б відповів гранично коротко,
Що не бачив Землі красивіше
І загадковіше, ніж Камчатка.
Низька до підніжжя лави,
Де сплітаються буваль і небиль,
І де на зріст людини трави. - Хлопці, а що таке Берінгія? (Це традиційна гонка на собачих упряжках, яка проводиться з 1990 року.)
- Хлопці, а що таке Берінгія? (Це традиційна гонка на собачих упряжках, яка проводиться з 1990 року.)
Цього року Беригиня відбулася з 7 по 21 березня.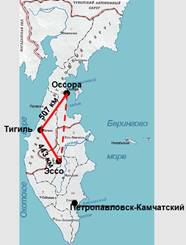 Берінгія стартувала із села Ессо, і одним із пунктів зупинки стало селище Тігіль. Відстань між цими населеними пунктами 443 км. Далі каюри вирушили до селища Оссора. На якій відстані від села Ессо може знаходитися селище Оссора, якщо відстань між селищем Тігіль та селищем Оссора 507 км?
Берінгія стартувала із села Ессо, і одним із пунктів зупинки стало селище Тігіль. Відстань між цими населеними пунктами 443 км. Далі каюри вирушили до селища Оссора. На якій відстані від села Ессо може знаходитися селище Оссора, якщо відстань між селищем Тігіль та селищем Оссора 507 км?
Учні відповідають на запитання вчителя, будують трикутник у робочому зошиті та висловлюють свої гіпотези, наприклад, відстань між с. Ессо та п. Оссора менше 950 км. Основною фігурою у розглянутій проблемі є трикутник. Я впевнена, що ви дуже спостережливі. Скажіть, а де ще у повсякденному житті вам траплялися трикутні форми? В архітектурі? (Знак аварійної зупинки тощо. Дахи мають трикутну форму.)
Основною фігурою у розглянутій проблемі є трикутник. Я впевнена, що ви дуже спостережливі. Скажіть, а де ще у повсякденному житті вам траплялися трикутні форми? В архітектурі? (Знак аварійної зупинки тощо. Дахи мають трикутну форму.)
- Ви маєте рацію. Основу дахів складають похилі та горизонтальні балки, які з'єднані між собою та утворюють трикутник.
Давайте сконструюємо макети власних дахів. Уявіть, що смужки, які лежать перед вами – це балки для побудови даху будинку.
Побудуйте, використовуючи ці макети трикутники зі сторонами:
б) 7, 14, 7;
в) 5, 16, 7.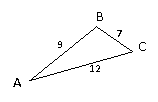 Вірна версія дітей:«Якщо сторона, побудована першою, менша від суми двох інших сторін, то трикутник будується».
Вірна версія дітей:«Якщо сторона, побудована першою, менша від суми двох інших сторін, то трикутник будується».
НД< АВ + АС, так как 7 см < 9 см + 12 см
АС< АВ + ВС, так как 12 см < 9 см + 7 см.
– Що пов'язують ці три нерівності? (Сторони трикутника.)
– Яка тема уроку? (Нерівність трикутника.)
– Сформулюйте цю властивість. (Кожна сторона трикутника менша за суму двох інших сторін.)
– Молодці хлопці, добре попрацювали, але попереду ще серйозна робота щодо доказу теореми.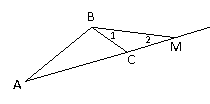 Дано: Δ АВС.
Дано: Δ АВС.
Довести: АВ<АС+СВ
Доказ:
Будуємо відрізок СМ, що дорівнює відрізку СВ на продовженні сторони АС.
У рівнобедреному ΔВСМ ∟1 =∟2
(за властивістю кутів у рівнобедреному трикутнику).
∟1< ∟АВМ, то ∟2<∟АВМ.
Розглянемо трикутник АВМ.
– Яким співвідношенням у трикутнику пов'язані сторони та кути? (У трикутнику проти більшого кута лежить велика сторона.)
- Яка сторона лежить проти кута АВМ? (Сторона АМ)
- Яка сторона лежить проти кута 2? (сторона АВ.)
– Порівняйте сторони АВ та АМ? (АВ< АМ)
АВ< АМ
АВ< АС + СМ
АВ< АС + ВС
Аналогічно доводиться, що ВС< АВ + АС;
АС < АВ + ВС. Теорема доказана.
Доцільно спочатку провести доказ теореми усно, а потім записати доказ на дошці та в робочих зошитах.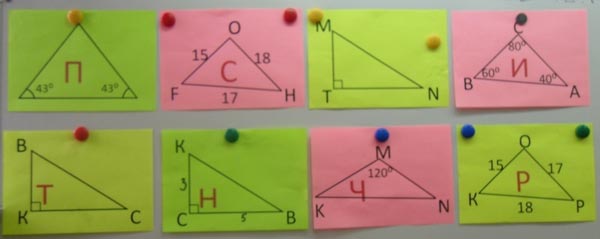

– Який трикутник є рівнобедреним? (П)
- У якому трикутнику більший кут? (Р)
– У якому трикутнику менша сторона ПС? (І)
- У якому прямокутному трикутнику катет ВК, гіпотенуза ВС? (Т)
– Який трикутник тупокутний? (Ч)
– У прямокутному трикутнику МNT назвіть кут, що протилежить катету ТМ (L N)П
Р
І
Т
Ч
І
Н
– Яку проблему я поставила перед вами на початку уроку? (Берінгія стартувала із села Ессо, і одним з пунктів зупинки стало селище Тігіль. Відстань між цими населеними пунктами 443 км. Далі каюри вирушили до селища Оссора. На якій відстані від села Ессо може знаходитися селище Оссора, якщо відстань між селищем Тігіль 507 км?)
– Запропонуйте вирішення цієї проблеми, використовуючи нові знання. (Відстань між Ессо та Оссорою має бути меншою, ніж 950 км.)
- Яку гіпотезу ми висували? (Відстань між Ессо та Оссорою має бути меншою, ніж 950 км.)
- Чи підтвердилася гіпотеза? (Так.)
- Що нового ви дізналися на уроці? (Будь-яка сторона трикутника менша за суму двох інших сторін.)
– Які властивості трикутника повторили? (У трикутнику проти більшої сторони лежить більший кут, і назад. У прямокутному трикутнику гіпотенуза завжди більша за катет. Якщо в трикутнику два кути рівні, то трикутник рівнобедрений.)
- Як називається гонка на собачих упряжках? (Берінгія.)
– З якого села стартує? (Із села Ессо.)
– У якому селищі фініш? (У селищі Оссора.)
– Як звати переможця 2011 року? (Андрій Прітчин.)
- Які цілі ми ставили на початку уроку? Чи досягли їх? Яку життєву проблему вирішили?
– Які проблеми виникли у вас на уроці? Як ви їх долали? Чи зрозуміла вам тема уроку? (Хлопці відповідають питання вчителя, беруть участь у рефлексії.)
– А тепер ще раз зосередьтеся на своїх відчуттях та емоціях, на тому, наскільки зрозуміла вам тема уроку, візьміть відповідний смайлик ( Додаток 2
), і повісьте його на дошку.
– Дякую, хлопці, за роботу! Урок закінчено, до побачення! Успіхів вам і перемог.